Návrhy střech – základní technické informace
Plochy střech věží - troj, čtyř a mnohoúhelníky
15. 8. 2016
PLÁŠŤ HRANOLU
Hranol (neboli Prizma) je těleso omezené částmi rovin, z nichž dvě jsou shodné, rovnoběžné a jmenují se základny. ostatní jsou rovnoběžníky a nazývají se bočními stěnami nebo také boky hranolu. Kolmou vzdálenost základen nazýváme výškou. Podle tvaru základen rozeznáváme hranol troj-, čtyř-, pěti-, šesti-, osmiboký atd..., dále hranol kolmý, jehož hrany leží kolmo k základnám, a hranol šikmý, s hranami nebo stěnami šikmo k základnám. Má-li kolmý hranol pravidelné základny, nazývá se hranolem pravidelným, jiný je nepravidelný. Zvláštním případem čtyřbokého hranolu je kvádr, omezený šesti pravoúhelníky (o základnách čtvercových nebo obdélnikových) a krychle, omezená šesti čtverci.
Plochu pláště pravidelného hranolu, kvádru o základnách čtvercových, a krychle zjistíme tak, že násobíme délku obvodu základny hranolu, tj. šířku pláště, výškou boční stěny.
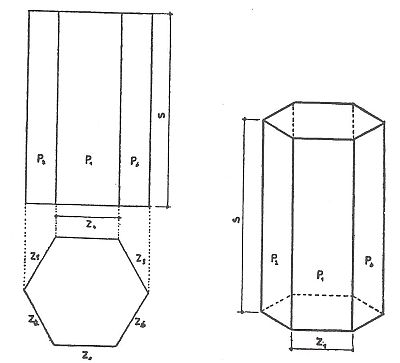
P=zh x s (při čemž -zh- = celkové délce základny hranolu rozvinutého pláště, -s- = výška boční stěny hranolu).
Jiný způsob je, že si vypočteme plochu jedné boční stěny a výsledek násobíme počtem bočních stěn. Tak např. plocha pláště kvádru o základnách čtvercových
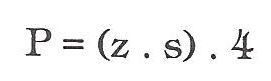
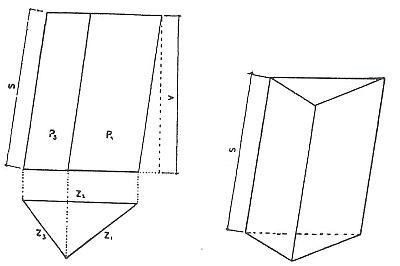
Plocha pláště nepravidelného hranolu rovná se součtu všech ploch bočních stěn. Tak např. plocha pláště šestibokého hranolu
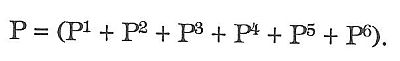
PLÁŠT JEHLANU
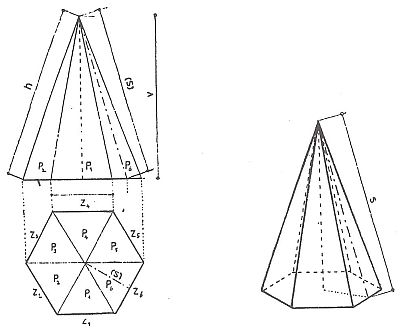
Jehlan (pyramida) je jednoduché těleso, omezené částmi rovin, z nichž jedna bývá troj-, čtyř- nebo mnohoúhelník a nazývá se základnou, ostatní jsou trojúhelníky se společným vrcholem a jmenují se boční stěny. Vzdálenost vrcholu od základny nazýváme výškou jehlanu. Podle tvaru základen rozlišujeme jehlan troj-, čtyř-, pěti-, šesti-, osmiboký atd. Jehlan, v němž kolmice spuštěná z vrcholu na základnu prochází středem základny se nazývá kolmý neboli přímý, jinak se nazývá šikmý. Kolmý jehlan se základnou pravidelného mnohoúhelníku a jehož všechny stěny o tvaru rovnoramenného nebo rovnostranného trojúhelníku jsou shodné se nazývá PRAVIDELNÝ. Jiné jehlany se nazývají NEPRAVIDELNÉ.
Plochu pláště pravidelného jehlanu, která představuje vlastně polovinu pláště pravidelného hranolu, vypočítáme tak, že násobíme délku obvodu základny povrchovou výškou jehlanu a dělíme dvěma. Např. plocha šestibokého jehlanu
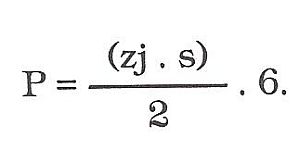
(přičemž -s- = povrchové výšce jehlanu, -zj- = celkové délce základny jehlanu rozvinutého pláště).
Jiným způsobem postupujeme, vypočítáme-li si plochu jedné stěny jehlanu tím, že základnu boční trojúhelníkové stěny vynásobíme její výškou a dělíme dvěma a výsledek vynásobíme počtem bočních stěn.
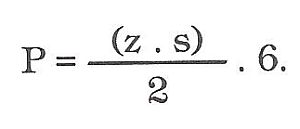
Plocha pláště nepravidelného jehlanu se rovná součtu všech ploch trojúhelníkových bočních stěn. Např. plocha u čtyřbokého nepravidelného jehlanu
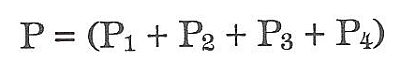
PLÁŠŤ JEHLANU KOMOLÉHO
Komolý jehlan je částí jehlanu mezi základnou a rovnoběžně k ní vedeným řezem, takže má dvě základny tvaru troj-, čtyř- nebo mnohoúhelníku o různé velikosti. Plochu pláště pravidelného komolého jehlanu, který se skládá ze stejných rovnoramenných lichoběžníků vypočítáme tak, že vynásobíme plochu jednoho lichoběžníku počtem bočních stěn. Např. plocha pláště čtyřbokého jehlanu
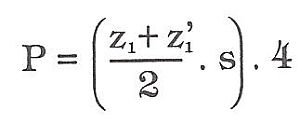
Anebo délky obvodů obou základen sečteme, dělíme dvěma a pronásobíme povrchovou výškou.
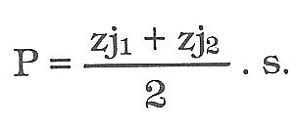
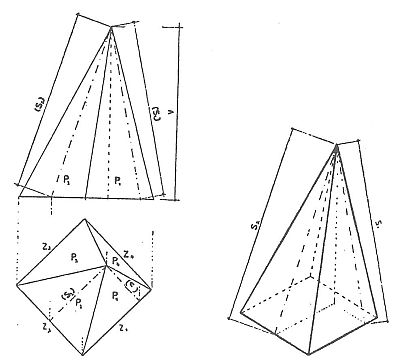
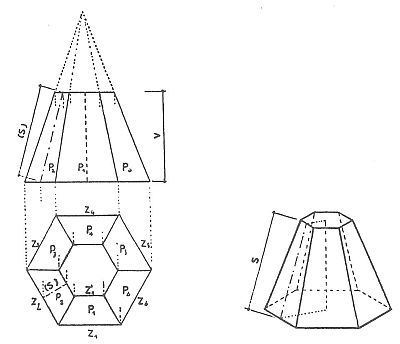
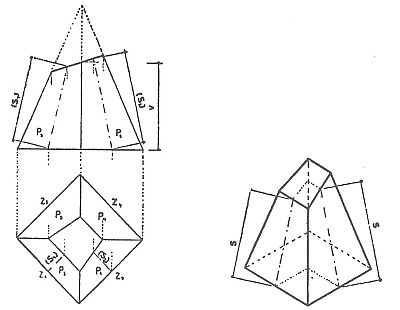
Plášť nepravidelného komolého jehlanu se skládá z nepravidelných lichoběžníků a plocha pláště se rovná součtu všech ploch bočních stěn.
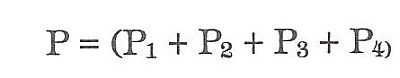
PLÁŠŤ JEHLANU O ZAKŘIVENÝCH BOČNÍCH STĚNÁCH
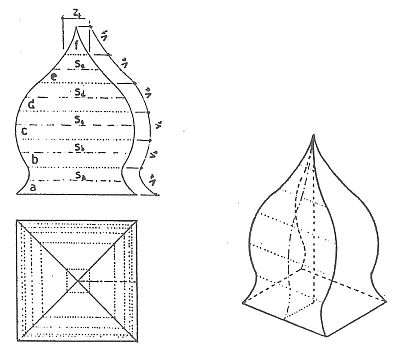
Základnou takového jehlanu bývá obyčejně čtverec nebo pravidelný mnohoúhelník, takže máme jehlan čtyř-, pěti-, šesti-, osmiboký (věž tvaru cibulovitého). Všechny boční stěny jsou stejné, takže k výpočtu plochy pláště stačí, když vypočítáme plochu jedné stěny jehlanu. K usnadnění výpočtu si plochu stěny rozdělíme pomocnými přímkami, které jsou rovnoběžné se základnou na menší plochy o tvaru rovnoramenných lichoběžníků. Poslední plocha u vrcholu se podobá tvarem přibližně rovnoramennému trojúhelníku. Vypočítáním všech ploch lichoběžníkových a ploch trojúhelníku a jejich součtem získáme plochu jedné boční stěny. Výsledek násobíme počtem všech bočních stěn a získáme tak plochu pláště. Např. plochu pláště čtyřbokého jehlanu vypočítáme podle vzorce
přičemž -a-, -b-, -c-, -d-, -e- nám představují plochy rovnoramenných lichoběžníků a -f- plochu rovnoramenného trojúhelníku, na které jsme si rozdělili jednu stěnu.
Autoři: Mikula Radovan, Řihák Jan M.
Zdroj: Publikace Pokrývačství Tradice z pohledu dneška, vydavatelství Grada


Autoři: Mikula Radovan, Řihák Jan M.
Zdroj: Publikace Pokrývačství Tradice z pohledu dneška, vydavatelství Grada

Rozdělili jsme více než 45 článků nabitých informacemi o střechách do přehledných témat, která vám
rychle pomohou se v problematice vyznat. Nestrácejte čas hledáním a mějte vše na jednom místě.

Krátké zprávy
-
Lehké střechy SATJAM opět na veletrhu Střechy-Solar-Řemeslo › více zde
-
12.2. 14.2.STŘECHY-SOLAR-ŘEMESLO - největší veletrh o střechách › více zde
-
Soutěž pro nejlepší klempíře - ART OF ZINC 2025 aneb Ukažte co umíte! › více zde
-
Co se děje s Novou zelenou úsporám a kdy se dozvíme, jak bude pokračovat? › více zde
-
CPS STAV: Rekonstrukce střech rodinných domů v Jihočeském kraji › více zde
Pro zákazníky
Rubriky článků
- Návrhy střech – základní technické informace
- Střešní krytiny
- Oplechování střech
- Fotovoltaika na střeše
- Střešní okna, světlovody a vikýře
- Okapové systémy - žlaby a svody
- Řemesla na střeše
- Rekonstrukce podkroví
- Zateplování střechy
- Krovy a dřevěné konstrukce
- Pergoly
- Střešní plášť odvětrání
- Ploché střechy
- Doporučené sklony střešních krytin dle ČSN (11/2020)
- Převodní tabulka sklonů + kalkulačka (2025)
- vzorkovník RAL
Rychlé hledání v katalogu
Zobrazit celý katalog
Střešní tašky: Benders, Besk, Betonpres, Bramac, Creaton, Erlus, Euronit, Eurotop, Filko, IBF, Jungmeier, KB Blok, KM Beta, Mediterran, Nelskamp, Roben, Sereni Coperture, Tondach, Walther
Vláknocementové šablony: Cembrit, Eternit Dacora, Eternit Alterna, Eternit New Stonit
Břidlice: Assulo, Dekslate, Richter-Pizarras, SSQ, Topstein, NSQ
Vlnité krytiny: Alinvest, Bituwell, Cembrit, Edilit, Eternit Baltic, Gutta, Haironvillevikam, Onduline, Onduroof, Onduvilla, Zenit
Plechové profilované krytiny: Alukryt, Balex Metal, Belprofile, Borga, Bratex, CzechCover, Dektile, Dektrade - Maxidek, Evertile, Evertech, Gerard, Hille, Isola, Keramet, KOB plechy, Lindab/Rova, Legos, Metrotile, Omak, Onduline, Planja, Powertekk, Prefa, Rheinzink, Ruukki, SAG, Satjam, Stato, Superal, Zambelli
Trapézové plechy: Balex Metal, Borga, Bratex, Bravo Smart Solution, Dekprofile, Haironvillevikam, Keramet, Legos, Lindab, Omak, Planja, Ruukki, Satjam
Falcované krytiny: Al plech Alinvest, Belprofile, Cu plech, Keramet, Lindab, Linedek, Nedzink, Prefa, Pz Plech, TiZn Rheinzink, VM ZINC, TiZn Celje, Bogner nerez
Bitumenové šindele: Akcept, Baros, CRC, Charvát, Technonicol, Guttatec, IKO, Isola, Katepal, Kerabit, Owens Corning, Tegola
Plastové krytiny: Capacco, Eureko, Gutta, Kretz, Lanit Plast, Naturaflex, Onduline, Pama, Polinext, Roofy, Tachovská Břidla, Taška Pyramida, Zenit
Krytiny z přírodních materiálů: Dřevěné šindele, Doškové střechy
Pomocný střešní materiál: Dřevěné latě, bednění, OSB desky, OSB desky Egger, Prvky odvětrání, Anténí tašky, Žlaby, Svody, Střešní výlezy











