Výpočty ploch střech - plochy jednoduché rovné - čtverec, obdélník atp.

8. 7. 2016

ČTVEREC

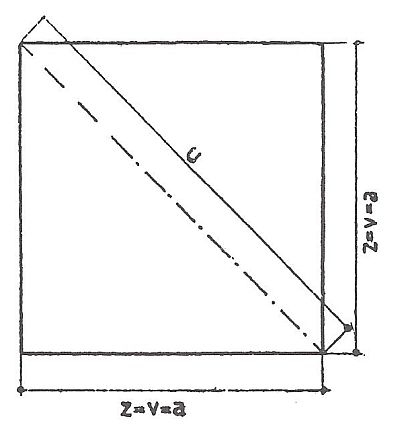
Má všechny čtyři strany stejně dlouhé s pravými úhly. Plochu vypočteme tak, že násobíme základnu výškou nebo stranu stranou, protože výška a základna (strany čtverce) jsou stejně dlouhé.

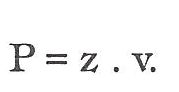
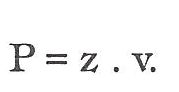
Vzorec pro výpočet plochy čtverce, zdroj: Grada

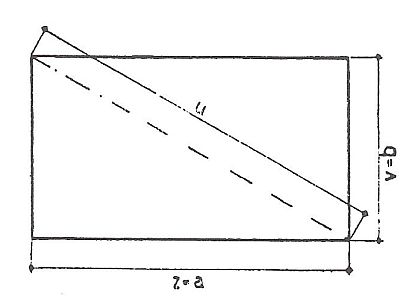
OBDÉLNÍK

Má vždy dvě a dvě protilehlé strany stejně dlouhé s pravými úhly. Plochu vypočteme tak, že násobíme základnu výškou.
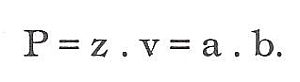
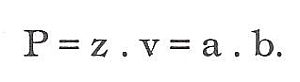
Vzorec pro výpočet plochy obdélníku, zdroj: Grada

KOSOČTVEREC

Má všechny čtyři strany stejné, vždy se dvěma ostrými a dvěma tupými protilehlými úhly. Plošně je to obdélník, jehož jednu stranu tvoří základna a druhou výška. Plochu vypočteme tak, že násobíme základnu výškou.
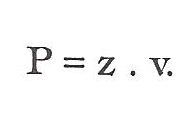
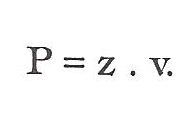
Vzorec pro výpočet plochy kosočtverce, zdroj: Grada

Vzorec pro výpočet plochy kosočtverce, zdroj: Grada

Výpočet plochy kosočtverce, zdroj: Grada

KOSODÉLNÍK

Má vždy dvě a dvě protilehlé strany stejně dlouhé se dvěma úhly ostrými a dvěma tupými. Plošně je to obdélník, jehož jednu stranu tvoří základna a druhou výška. Plochu vypočteme tak, že násobíme základnu výškou.
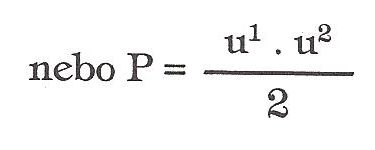
Alternativní vzorec pro výpočet plochy kosodélníku, zdroj: Grada

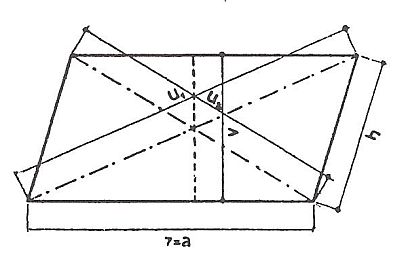
Výpočet plochy kosodélníku, zdroj: Grada

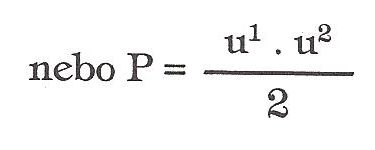
LICHOBĚŽNÍK ROVNORAMENNÝ

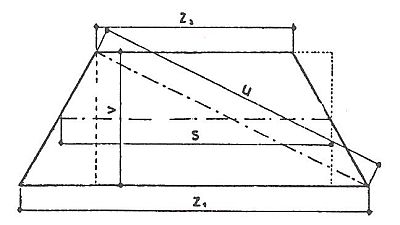
Má dvě protilehlé rovnoběžné strany nestejně dlouhé a dvě protilehlé strany (ramena) různoběžné a stejně dlouhé. Má dva úhly ostré a dva tupé. Plošně je to obdélník, jehož jednu stranu tvoří základna, vyjádřena střední délkou rovnoběžných stran a druhou výška lichoběžníka. Plochu vypočteme tak, že sečteme délky obou rovnoběžných stran, dělíme dvěma a výsledek násobíme výškou.
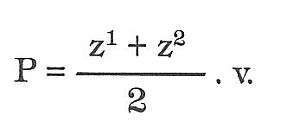
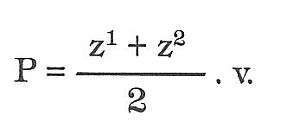
Vzorec pro výpočet plochy rovnoramenného lichoběžníku, zdroj: Grada

Vzorec pro výpočet plochy rovnoramenného lichoběžníku, zdroj: Grada

Výpočet plochy rovnoramenného lichoběžníku, zdroj: Grada

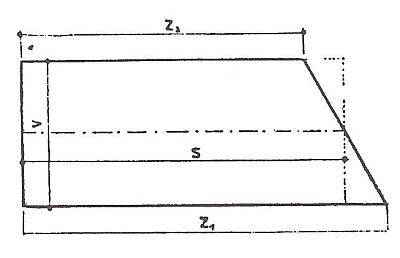
LICHOBĚŽNÍK PRAVOÚHLÝ

Má dvě strany rovnoběžné, dva úhly pravé, jeden tupý a jeden ostrý. Plochu vypočteme tak, že násobíme střední délku obou rovnoběžných stran výškou lichoběžníku.
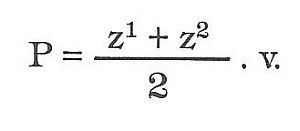
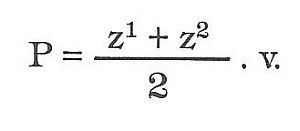
Vzorec pro výpočet plochy pravoúhlého lichoběžníku, zdroj: Grada

Vzorec pro výpočet plochy pravoúhlého lichoběžníku, zdroj: Grada

Výpočet plochy pravoúhlého lichoběžníku, zdroj: Grada

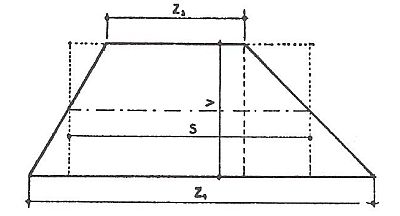
LICHOBĚŽNÍK NEROVNOSTRANNÝ

Má dvě strany rovnoběžné a nestejně dlouhé, dva úhly tupé a dva ostré. Plochu vypočteme tak, že násobíme střední délku obou rovnoběžných základen výškou.
Vzorec pro výpočet plochy nerovnostranného lichoběžníku, zdroj: Grada

Vzorec pro výpočet plochy nerovnostranného lichoběžníku, zdroj: Grada

MNOHOÚHELNÍK NEPRAVIDELNÝ (pěti-, šesti-, osmi-, dvanáctiúhelník atd.)

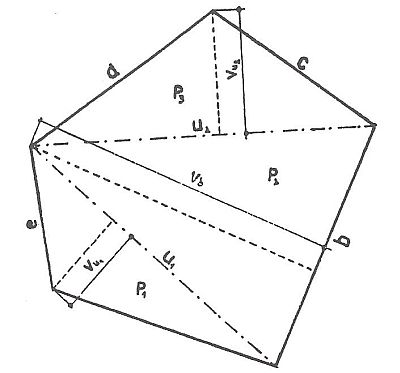
Jeho strany jsou různě dlouhé a součet vnitřních úhlů se rovná n-2x180° (n=počet stran). Nepravidelný mnohoúhelník si rozdělíme na několik trojúhelníků a vypočítáním všech trojúhelníkových ploch a jejich sečtením dostaneme plochu nepravidelného mnohoúhelníku. Jako např. nepravidelná plocha pětiúhelníku jako na obrázku níže.
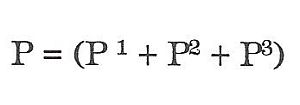
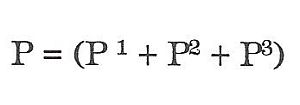
Vzorec pro výpočet nepravidelného mnohoúhelníku, zdroj: Grada

Vzorec pro výpočet nepravidelného mnohoúhelníku, zdroj: Grada

Výpočet nepravidelného mnohoúhelníku, zdroj: Grada

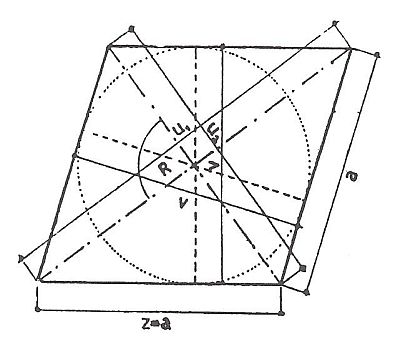
MNOHOÚHELNÍK PRAVIDELNÝ (pěti-, šesti-, osmi-, dvanáctiúhelník atd.)

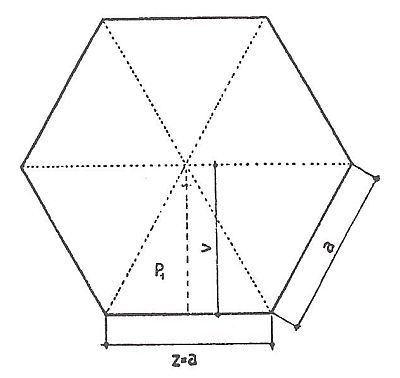
Všechny strany jsou stejné a součet vnitřních úhlů = n-2mx180°. Pomocnými přímkami, vedenými středem, si rozdělíme plochu na stejně velké trojúhelníky. Vypočteme plochu jednoho trojúhelníku a násobíme počtem všech trojúhelníků, čímž dostaneme plochu mnohoúhelníku. Např. plocha šestiúhelníku na obrázku.
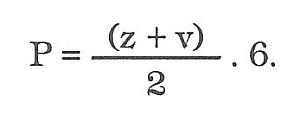
Vzorec pro výpočet pravidelného mnohoúhelníku, zdroj: Grada

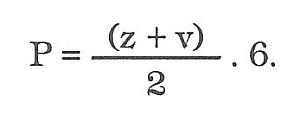
Vzorec pro výpočet pravidelného mnohoúhelníku, zdroj: Grada

Výpočet pravidelného mnohoúhelníku, zdroj: Grada

Autoři: Mikula Radovan, Řihák Jan M.
Zdroj: Publikace Pokrývačství Tradice z pohledu dneška, vydavatelství Grada

Obálka knihy Pokrývačství - Tradice z pohledu dneška, vydavateslství Grada

Rozdělili jsme více než 45 článků nabitých informacemi o střechách do přehledných témat, která vám
rychle pomohou se v problematice vyznat. Nestrácejte čas hledáním a mějte vše na jednom místě.